LH:000:RH
"{LH=Left Handed : Right Handed=RH : 000= All spots in conventional orientation}"
LH:000:RH
"{LH=Left Handed : Right Handed=RH : 000= All spots in
conventional orientation}"
There is probably more than you care to know about right and left handed coordinate systems and dice here, and there is yet more to be added.
A rotation
about a directed axis is called positive, or right-handed, if it
causes a right-handed screw to advance in the positive direction
of the axis.
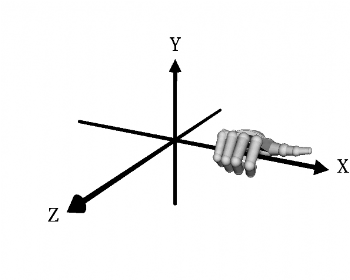
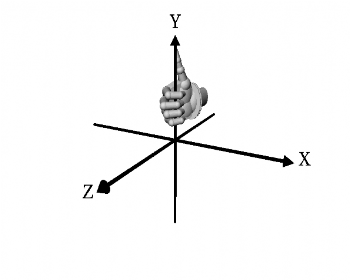
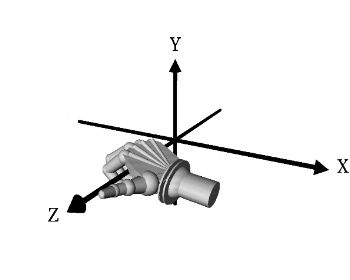
The three images above show a standard right-handed coordinate system with right-handed rotation about each axis.
If a three axis orthogonal coordinate system has ordered axes
the system will be right-handed if right handed motion along the
It is the standard right hand rule for physics, math, or engineering. It's the same coordinate system that is used by AutoCAD which was used to render (shade) the dice images presented here.
There are difficulties in transmitting information about right- and left-handedness. This is a fundamental natural problem. I developed a rotation function for a left-handed coordinate system more than 30 years ago. The function is called "RLH" (an abbreviation for Rotate-Left-Handed). It works fine in right-handed systems as well, as long as the 1,2,3 ordering convention is kept consistent. In practice, right-handed is right-handed because most people tend to prefer right handed operations for strength and dexterity. That is why a right-handed baseball glove is worn on the left hand???
References to RH and LH Dice
https://en.wikipedia.org/wiki/Dice
Opposite sides of a modern die traditionally add up to seven, implying that the 1, 2 and 3 faces share a vertex. The faces of a die may be placed clockwise or counterclockwise about this vertex. If the 1, 2 and 3 faces run counterclockwise, the die is called "right-handed", and if those faces run clockwise, the die is called "left-handed". Western dice are normally right-handed, and Chinese dice are normally left-handed
This results in the same definition I have used above.
https://boardgamegeek.com/geeklist/164435/left-handed-dice
A sample showing a right-handed and left-handed dice [This definition is the same as the vector definition I use.]
On rare occasions, I have found dice with the "two" spots horizontal or vertical when the "one" spot is on top. These are so rare that there are probably not enough dice in existence to complete a set of 32 dice with all the combinations using 2H and 2V in addition to the "conventional" spot variations.
The above statement about horizontal and vertical twos is still probably true for machined dice or plastic dice that are cast in a single mold. It turns out that panted dice or handmade dice have enough variability to complete a set. It seems that dice produced for East Asian consumption have more horizontal and vertical twos. I cannot confirm this, but this would explain why horizontal and vertical twos get to the United States, because an Asian manufacturer would not recognize a horizontal or vertical two as being odd or strange.
Until I found a complete set of horizontal and vertical twos, all in a single set of ten packages of six dice each, I had only collected about six of the possible sixteen variation of horizontal and vertical twos. The only other big find of variations of dice spots was in a set of wooden dice that were hand carved from driftwood (a game store in San Clemente, California)
There are spherical dice (right handed) which are double layer plastic with three orthogonal internal bored shafts and a ball bearing. The die (casting) marks on the outside of the spherical dice indicate a common mold and manufacturer, but I don't know who actually makes them. I would like to get drawings or find out how the original designer decided to locate the spots on the dice.
Role playing cubical dice use arabic numerals on each face and have the common element of the opposite sides adding up to seven. Because the numeral are asymmetric, there are 4**5=1024 combinations of possible in a collection of right handed dice or 2048 combinations including right and left handed dice. The effort to locate such a collection is prohibitive. I have located both right and left handed role playing dice, but do not intend to make a collection. There are probably less than 2048 manufacturers of role playing dice and it is very unlikely that a complete collection even exists (unless a set were deliberately produced).
Quoted from William F. Borland (1992) The Gambler's Mail Order Magalog, Las Vegas, Nevada
It seemed that if the imbalance statement were true, then rolling dice and determining the statistical variation would be a good science fair experiment requiring statistical analysis.
A series of 100 throws of sets of 5 dice were made with eight sets of dice. That's 4000 rolls altogether. Drew Danley did all the rolling and recording. The dice are ordered in what we had thought would be decreasing randomness. We could not distinguish between any of the dice and random variation, except for the loaded dice. I learned about unreliable uses of computer generated random numbers after it took me a long time to get the performance of a computer simulated craps game to come out like the calculated odds. Drew's efforts won a 1st place in his school science fair and a 2nd place in the county science fair.
The best odds in any casino dice game that a player can get is in craps, where the best odds are 0.7% against the player. It seems that unbalanced dice should not be noticeable if their effect is much less than half that amount. (For annual percentage rate, try raising 1.007 to the Nth power [1.007**N=???] where N is the number of craps throws on a single casino table in a year. If you do this on a hand calculator, it will overflow!!)
Calculating the mass imbalance on a standard dice, if the dice is balanced on the 1-2 edge, the 6-1 imbalance is equivalent to a tilt of about 0.3 degrees to get back to balance. The 5-2 imbalance is about 3/5ths in the opposite direction. The net imbalance is only about 0.12 degree out of 90 degrees possible rotation, or about (0.12/90=0.0013). The best possible odds in casino dice is 0.007 (in favor of the house). The imbalance error is about 5 times below that level on normal dice because of the hollow spots.
For the loaded dice, balanced on an edge where favored number will come up, about 60 degrees of range favors the loaded number. This is an unbalance favoring the loaded number about 2/3 or 0.67, about 100 time the factor of concern.
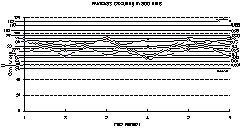(10k)
In 500 throws, any spot should come up 500/6=83.3 times.
All but the loaded dice are plotted in this Excel graph.
Questions after the first experiment:
After thinking about the above results for a while, one of the variables was that eight different types of dice were used. What if manufacturing imbalances were different for the different types? The Loaded dice were known to be imbalanced and were not plotted in the data. The hand made revolutionary dice were clearly asymmetrical, but did not seem unusual by looking at the roll results. The cheap dice and the spherical dice were most likely to be imbalanced also.
Another science fair experiment was done by rolling a single set of five Bicycle Dice and a set of five Casino Dice (serial no 409). The Bicycle Dice (Model # DCE) are about as standard as non-casino dice as are available. The Casino Dice are high precision machined and intended to be uniform and balanced by having filled spots.
The dice were rolled five at a time in sets of thirty rolls by John Cox for a science fair display in February 2001. This was nominally equivalent to 150 roll of a single dice.
This was repeated three times for a total of 450 rolls for each type of dice. The results of the rolls were plotted in groups of 150. Each spot value should have occurred about 25 times each. When we looked at the data by groups of 150, there was very little evidence of any trends. If anything, the Bicycle Dice seemed to show a little less dispersion than the Casino Dice.
The experiment was repeated three more times for another 450 rolls for each type of dice. When all six sets of each type of dice were plotted, they looked similar, but there seemed to be a 1 through 6 trend in the Bicycle Dice sets. This trend seems clearer when the entire sets are added together. There should then be 900 rolls of each type of dice, with about 150 rolls of each number.
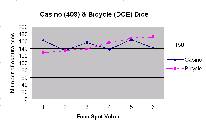The data show a trend for the Bicycle Dice, but just outside the variability shown for the Casino Dice. The implication is that it really takes hundreds of throws for the spot imbalance to show up. The experiment needs to be repeated with about 2000 rolls to see if the trend repeats.
In casino gambling games, the plays are so short and the odds are so heavily stacked in favor of the house that there would be no real advantage or disadvantage of using the Bicycle type dice with the imbalanced holes.
John Cox and the Science Fair Experiment.
Standard, common, casino convention spots are taken as the baseline for right handed dice. Hoyle or Milton Bradley 5/8 inch dice are uniformly right-handed, as far as I know.
I have never been able to find out why the spots are configured the way they are. I called someone at Milton-Bradly and they don't even have a dice drawing, they just order 5/8 inch white dice with black spots and get millions of right-handed dice. Someday this may change and no one will likely even notice.
For spot variations, I have chosen to assign numbers for the
spots which are rotated. For example, in the sequence which is
shown on this page, the normal dice are labeled "000".
With the 2 only rotated, I would call the set (RH2) or (LH2) and
have labeled the imaged "002", etc. The sets on this
page are numbered so they correspond to a binary counting
sequence to show that all combinations are present:
000, 002, 030, 032, 600, 602, 630, 632 which correspond to the
binary sequence
000, 001, 010, 011, 100, 101, 110, 111 the eight combinations
equivalent to the numbers 0 through 7.
"{LH=Left Handed : Right Handed=RH : 000= All spots in conventional orientation}"
LH: 000 :RH
LH: 002 :RH
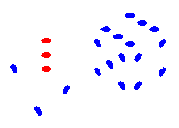LH: 030 :RH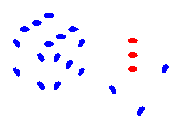
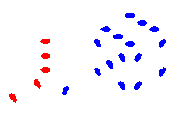LH: 032 :RH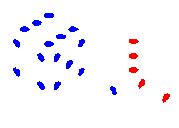
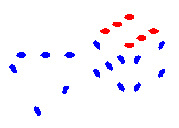LH: 600 :RH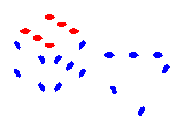
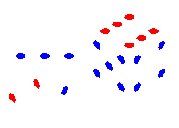LH: 602 :RH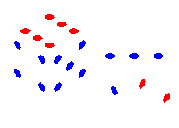
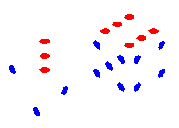LH: 630 :RH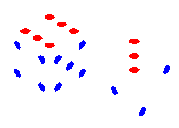
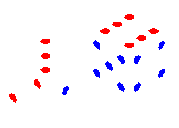LH: 632 :RH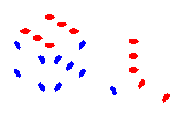
Added convention for horizontal and vertical "two"
Horizontal[..]=0 or standard; Vertical[:]=rotated or 1 (vertical like a "1").
I have assembled a collection of right- and left-handed dice with spots in all the configurations shown above (including all the variations of horizontal and vertical twos as well). It's probably the largest (only) collection of left-handed dice in the world. There are very few people who even know there are left-handed dice, including most, if not all manufacturers of left-handed dice. The collection of standard dice (diagonal twos) took three or four years to assemble, visiting game stores all over the United States while on travel (California, Florida, Colorado, Indiana, Maryland, Pennsylvania, Virginia, District of Columbia). After collecting the dice variations for about twenty-five years, I had only collected about a half a dozen of the sixteen variations of the horizontal and vertical two dice, then one day in 2010 I found a complete set of horizontal and vertical two dice in ten sets of six dice each purchased from Dollar Tree!
For images of these dice, go to dice collection.
Common Dice are mostly Right Hand 000
By sheer abundance, the most common occurrence of dice is RH000. I have not counted precisely, but RH000 probably account for 99% of all occurrences. Milton Bradley & Yatzee account for millions of RH000 dice per year. Probably more than 99.9% of Casino Dice are RH000. I have found only two exceptions to RH000 in casino dice. One is some of Harrahs Casino Dice (RH230, but probably most are RH000) and some of Caesars Palace Dice (RH230). I have not seen any other variation in casino dice, except in pictures (drawings, not photographs) of casino dice which will quite frequently have a Right Handed and Left Handed die in the same picture. I have seen photographs from museums where there is a hand made right handed and left handed die in the same photograph. Even if the negative were reversed, the dice would still be opposite handed.
Cheaper dice come in more varied occurrences. Usually all of a production run are the same. Mostly cheaper dice are RH000, but exceptions are not rare. Printed dice, where it looks like opposite sides are printed at the same time change from RH to LH depending on how they are handled in production. I have found printed sets of five dice that have several variations and both RH and LH dice in the same set of five.
Casino Dice that are not RH000
Roger Zimmerman sent me an e-mail with information that some Harrah's dice were not RH000 dice. I looked at all the Harrah's websites and found the following pictures. I heard from someone that Caesars Palace had different dice also. I found confirming evidence in a picture on one of their websites. I wonder if these variations are deliberate or accidental - does anyone know?
Caesars Palace RH230 dice
Harrahs RH000 dice
Harrahs RH230 dice
Harrahs RH000 dice
Dice Images (Virtual Dice)
For images of dice collected off the Internet, go to dice image collection.
If you have any more information on right or left handed dice or have some samples you can send me, I can be reached at E-Mail: D.C.Evans@EvansOpticalEngineering.com